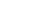What is the least common multiple of 12 and 40? (LCM of 12 and 40)?

What is the Least Common Multiple of 12 and 40?

The Least Common Multiple (LCM) of 12 and 40 is the smallest positive number that is a multiple of both 12 and 40.

Here we will show you two different ways to figure out the Least Common Multiple of 12 and 40.

Our favorite way is to find the prime factors of each number and then merge them together to get the answer.

The prime factor(s) of 12 are:
2 x 2 x 3

The prime factor(s) of 40 are:
2 x 2 x 2 x 5

Merging them together using the least amount of factors, you get:

2 x 2 x 2 x 3 x 5

Then you can multiply those numbers together to get the Least Common Multiple (LCM) of 12 and 40 as follows:

120

To find the Least Common Multiple of 12 and 40, you can also make a list of multiples of 12 and a list of multiples of 40.

Multiples of 12 would be 12, 24, 36, 48 and so on.

Multiples of 40 would be 40, 80, 120, 160 and so on.

Now, compare the two lists to find the smallest number the two lists have in common, which is the Least Common Multiple of 12 and 40. You will once again see that the answer will be:

120

Least Common Multiple Calculator
Enter another two numbers below to find the Least Common Multiple

What is the Least Common Multiple of 12 and 41?
Go here for the next Least Common Multiple on our list that we calculated.

We used used the following sources to solve the problem on this page:

Prime Factorization of 12

Prime Factorization of 40

Multiples of 12

Multiples of 40